tomgalvin.uk

I’m currently trying my hand at creating a programming language. Naturally, one of the initial stages of doing such a thing is to write a reference compiler (or interpreter), to show that the language is usable. The interpreter I’m writing is in C, and has proved challenging (having no prior experience or formal education in parsers or formal language theory); I’ve learned a few things just from writing the lexical analyser and the parser, one of which I want to share with you.

The parser I wrote is a hand-written recursive descent parser, being perhaps the only type of parser suitable for writing by hand. The main problem with recursive-descent parsers (and, indeed, all parsers in the LL(k) family) is that they cannot parse some grammars - or at least not naïvely. Take for example this BNF grammar representing addition, multiplication and exponentiation.

  <expr-single> ::= "(" <expr-sum> ")" | <integer>
<expr-exponent> ::= <expr-single> "^" <expr-exponent> | <expr-single>
 <expr-product> ::= <expr-product> "*" <expr-exponent> | <expr-exponent>
     <expr-sum> ::= <expr-sum> "+" <expr-product> | <expr-product>

This grammar is perfectly valid; given a suitable parser, such as an LALR parser produced by yacc, one could parse an input token stream such as 3+2^(1+4*3)+4 to produce a tree like this.

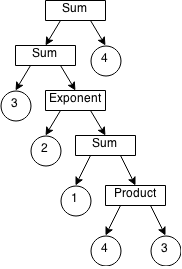
left recursion

Now let’s look at some of the issues with using LL(k) parsers to parse such an expression - specifically, using a recursive descent parser. Let’s try to think of a recursive-descent parsing procedure to generate the abstract syntax sub-tree for the expr-sum production. As the production is immediately recursive (or left recursive), it can potentially be expanded (or rewritten) infinitely many times. The rule initially takes one of two alternative forms, indicated by the pipe |:

<expr-sum> ::= <expr-product>
           ::= <expr-sum> "+" <expr-product>

The second form contains <expr-sum> and can thus be rewritten again into a further two forms:

<expr-sum> ::= <expr-product> "+" <expr-product>
           ::= <expr-sum> "+" <expr-product> "+" <expr-product>

Again, the second form still be rewritten into a further two forms. It’s clear that the rule can be expanded as many times as you like, producing a substitution for <expr-sum> that can have an unbounded number of alternative forms. The problem arises when you attempt to decide which of those forms to use - how can you tell just by looking at the first token in the input? The first two tokens? The first k tokens? Writing a parser with unbounded token lookahead is possible, but perhaps not practical in the case of hand-writing a conventional parser. This issue is known as a FIRST-FIRST conflict. The first tokens of all of the possible alternative forms are the same, meaning the parser cannot know whether to stop recursing or carry on. This is a limitation of predictive parsing - parsers that know ahead of time which production to use by looking a certain number of tokens ahead, without back-tracking on themselves. LR(k) and similar parsers are not predictive parsers, so they don’t suffer from this limitation.

One solution to this is to alter the grammar to a form where the first tokens of the two alternative forms differ. This introduces another non-terminal:

        <expr-sum> ::= <expr-product> <expr-sum-further>
<expr-sum-further> ::= "+" <expr-product> <expr-sum-further> | ε

Where ε denotes no token; ie. <expr-sum-further> can expand to nothing. This now means the first tokens of <expr-sum> and <expr-sum-further> differ; <expr-sum-further> begins with the addition symbol or nothing, meaning the production for <expr-sum> ends once a symbol other than + appears after <expr-product>. We have moved the recursive part of the production from the left (which causes the problems) to the right (which lets us know whether to stop recursing or not). This is called left-factoring, and is expressed rather succinctly by the Dragon Book¹ as the following.

A ::= Aα | β

is equivalent to

A ::= βB
B ::= αB | ε

However, even though the grammar can now be parsed, the generated parse tree is subtly different. When the grammar changed from left-recursive to right-recursive, it also changed from left-associative to right-associative. Associativity describes how grouped expressions are parsed. Addition, is by convention left-associative, meaning 1+2+3+4 is normally understood as ((1+2)+3)+4 and not 1+(2+(3+4)) - exponentiation however is by convention right-associative, meaning 1^2^3^4 is understood as 1^(2^(3^4)).

This makes no difference to the result when, like addition, the operation is commutative - order of calculation does not matter. However, this makes a large difference with operators such as subtraction: ((1-2)-3)-4 equals -8 whereas 1-(2-(3-4)) equals -2. This means the resulting parse tree is incorrect.

Two parse trees for the input `α-β-γ-...-δ-ε`. Shown is the left-associative parse tree (left) and the right-associative parse tree (right), where the left-associative tree is correct.

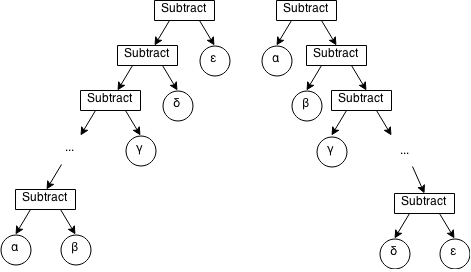
There is, however, a solution. I believe this scenario is a prime example where our notation impedes our understanding of a concept. Backus-Naur Form, as it originally was, allows the repetition of a series of tokens only via recursion. An alternate method would be to show iteration instead - Extended Backus-Naur Form represents this with curly braces, {…}, where everything in the braces can be repeated zero or more times. Thus, our production for <expr-sum> becomes:

<expr-sum> ::= <expr-product> { "+" <expr-product> }

A pseudo-code algorithm representing the generation of the parse tree for <expr-sum> in a recursive-descent parser can be written as follows.

Function ParseSum():
  SumTree ← ParseProduct()
  While Accept("+"):
    SumTree ← Sum(SumTree, ParseProduct())
  Return SumTree

This will generate a parse tree of the correct associativity. To understand how this function works, think of the original left-recursive production for <expr-sum>:

<expr-sum> ::= <expr-sum> "+" <expr-product> | <expr-product>

What this iterative pseudo-code algorithm essentially does is parse this production from the bottom-up. The procedure starts with the <expr-product> form of the production, and then applies the <expr-sum> "+" <expr-product> form as many times as it can before stopping. In this way, the function is reminiscent of a miniature LR parser, by continually reducing the first form of the production as long as “+” is shifted.

right recursion

The second half is not essential to writing a recursive-descent parser. To parse a right-associative rule such as <expr-exponent>, a right-recursive rule will work fine in most cases. The production for <expr-exponent> is the following:

<expr-exponent> ::= <expr-single> "^" <expr-exponent> | <expr-single>

This can be represented in a recursive-descent parser like this:

Function ParseExponent():
  ExponentTree ← ParseSingle()
  If Accept("^"):
    Return Exponent(ExponentTree, ParseExponent))
  Else:
    Return ExponentTree

Such a parser works - however, if the parser throws an exception at some other part of the program, and the expression parsed has many nested exponents like 4^4^4^4^4^4^4^4^4^..., then the ParseExponent() function will be called as many times as there are exponents, meaning you will have a stack trace looking like the following:

...
in ParseExponent():73
in ParseExponent():73
in ParseExponent():73
in ParseExponent():73
in ParseExponent():73
in ParseExponent():73
in ParseExponent():73
...

In the best case scenario, it looks ugly. In the worst case scenario, it leads to a stack overflow. For consistency’s sake I wanted to create an iterative parser for right-recursive productions, in the same way I did for left-recursive productions. The upside of this method is that it is not self-recursive; the downside of it is that it requires a pointer type.

What the algorithm does is store a pointer, representing where the next parsed sub-tree is to be inserted into the exponent tree. The pseudo code algorithm looks like this, using C-style pointer syntax:

Function ParseExponent():
  ExponentTree ← ParseSingle()
  Bottom ← &ExponentTree
  While Accept("^"):
    RightTree ← ParseSingle()
    *Bottom ← Exponent(*Bottom, RightTree)
    Bottom ← &RightTree
  Return ExponentTree

This builds the tree from the top down, where the pointer stores the location of the current bottom of the tree. The pointer is needed as the function must return the top of the tree while still keeping track of the bottom; the pointer is not needed for a left-associative function such as ParseSum() where the tree is built from the bottom up, as the tree node generated last is also the tree node returned from the function, meaning only one variable SumTree is used to keep track of the top of the tree.

Of course, both of these iterative solutions still produce a parse tree that needs to be analysed. The semantic analysis may still be recursive - or, alternatively, you may apply the principles in this post to iteratively ‘unwind’ the parse tree during analysis. I’ve written a sample recursive descent parser to demonstrate the algorithms in this post. It’s written in C, and accepts the arithmetic grammar at the top of the post, generating the corresponding parse tree. Feel free to adapt the code for your own purposes or use it as a learning/teaching resource. The source code can be downloaded here: recursive-descent-parser.c

I’m not sure if the right-recursion iterative parser already exists in practice. I know that the left-recursion iterative parser does. However as far as I’m aware the pointer-based algorithm for parsing right-recursive rules is new, at least in the way that I have written it.