The type system in JavaScript is undoubtedly quite different from a run-of-the-mill OOP language. Of course, this is probably because JavaScript is indeed not object-oriented - rather, it has a prototype-based object system, in which you can imitate classes with some weird, somewhat non-idiomatic code. I’ve never quite understood the behaviour of the prototype system, so I decided to write something to force myself to use it.
When writing JavaScript code in the past, I’ve made a nasty habit of avoiding the prototype system entirely - meaning I ended up using lots of standard objects and arrays everywhere to store data, which is certainly not fantastic. This is the reason why I’ve decided to do this. The project I’ve made simulates a 2-dimensional transverse wave in a little wave box. The waves are rendered using SVG (lazy, I know), with green and red representing up and down (positive and negative, in and out, or whichever pair of antonyms you’d like).
The physics behind the simulation is very simple: imagine a static grid in 3-D space.

Onto this grid, place a mass attached by a spring.

The physics behind a spring is very simply modelled by an equation known as Hooke’s law - the force exerted on the mass by the spring is the product of the distance (x) of the mass from the equilibrium (zero displacement) point, and a constant k (the spring constant) which is an attribute of the spring. The force is in the direction toward the equilibrium point, so this equation can be written as F=-kx. This means that, if the mass is a little bit upward, it’s forced a little bit downward. If the mass is very high up, a very strong downward force is applied - and vice versa for down and up. So our mass on the grid will look like this after some time:

Of course, this up-down forcing mechanic means the mass will oscillate up and down. For this reason, this type of system is called a simple harmonic oscillator, and has some nice equations to describe it. As our mass only ever oscillates in one axis, we only need three values to represent each oscillating mass: the displacement of the mass from the equilibrium center point, the velocity of the mass (ie. how much the displacement will change per second), and the mass of the oscillating body itself. We could in theory have a different spring constant for each spring, which would made the wave act non-uniformly through the grid, but for the sake of this explanation I haven’t done that.
Now to simulate a wave, we need to somehow connect all of these masses together in such a way that neighbouring masses are pulled toward each other, to simulate a “Mexican wave” of masses on the grid, like this:
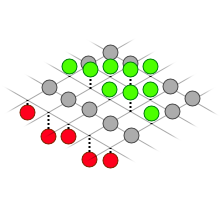
The simplest way that I have found to model this is by connecting each mass to each neighbouring mass by another spring. These springs behave the same as the other springs, except that Newton’s 3rd law must be taken into consideration - ie. the masses are forced toward each other with equal magnitude. Otherwise, we’d slowly build up momentum from nowhere.

Now, having the equations is all well and good, but simulating them is a challenge in itself. Upon starting this project I used the naive method of simply adding the rate of change of velocity (acceleration), multiplied by the time step, to the velocity each second - likewise for the displacement. This is called Euler’s integration method, and while it works for very simple simulations, the result of using Euler’s method diverges from the actual scenario significantly for complex situations.
I’ve instead had to implement a method known as fourth-order Runge-Kutta integration. This works with a slightly more involved approximation method, that tentatively steps forward in time and corrects for any miniscule changes in acceleration and position beforehand, that Euler’s method would otherwise ignore. I don’t understand the maths behind the derivation of this method, but it works, and the wave simulator uses a four-pass integration to step forward in time.
The end result of this is a wave simulator that works surprisingly well. The display is a simplified top-down view of the grid displayed above.
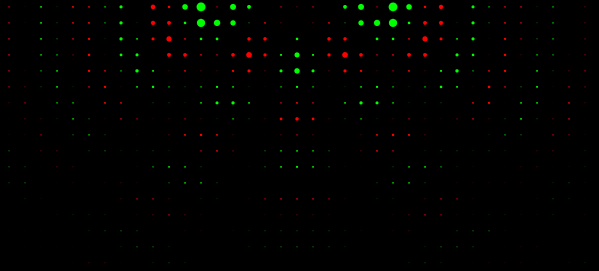
There are some caveats to this simulator.
- The simulation is slow. I’ve only tested the simulator on Firefox on a slow Windows box, and an HTC One M8 in Chrome (which worked, but only on the coarsest resolution.) This is probably due to the SVG rendering being done by software in the browser, and my not-too-efficient implementation of the RK4 integrator.
- The simulation is not completely stable. It is much better than it was with Euler’s method of integration, but given enough time, the waves will eventually devolve into a weird looking pattern that looks like an erratic standing wave. However, it has been brought to my attention that this is because…
- The waves produced are not perfectly circular. Someone pointed this out to me on Reddit and I initially assumed that it was standing waves being formed - however it seems that the behaviour is an artefact of each mass only being connected to the 4 directly neighbouring masses. Perhaps connecting each mass to all 8 surrounding masses - with lower spring constants for the corner-touching oscillators - would improve the stability of the simulation.
Anyway, if you want to try out the simulator yourself in the browser, you can try it on this website, or view the source code on GitHub.