Today’s hard DailyProgrammer challenge is quite a stinker of a challenge. It’s the inverse of Wednesday’s intermediate challenge, and is essentially two problems in one. Specifically, this is a constraint satisfaction problem (thanks to /u/code_and_theory on Reddit), and they can typically be solved by backtracking search algorithms, which is what I’ve used in my solution. You’ll be given a board of characters, like this:

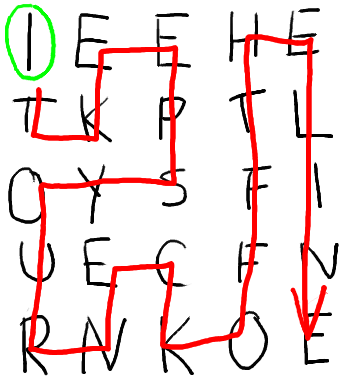
Next, you’ll be given a starting position on the board. In this particular case, it’s the top left - position (1, 1).

Now, your task is to find a complete (ie. Hamiltonian) path through this grid which, when read out from start to finish, forms a valid sentence. Pretty hefty task. In this case, the sentence follows this path:
The best way to break this down is to solve it in two stages.
valid sentences
Our first task is to determine if a string is a valid sentence of words in English. To do that, we’re going to need a list of words. I used this word list because the built-in one in Arch is fairly useless, as it contains every letter of the alphabet individually, which aren’t valid words. Let’s look at a simple sentence. We’ll use lower case for un-resolved bits of the sentence, and space-delimited UPPER CASE for bits of the sentence that we know are valid words.
thereissomethingafoot
The fundamental step is to see which words could form the start of this sentence. In this case it could be the or there:
THE reissomethingafoot
THERE issomethingafoot
Now, let’s look at both of these cases to see where we can go from here. The first possiblility starting with the could have Reiss as the next word:
THE REISS omethingafoot
After this, we’re stuck - OMETHINGAFOOT doesn’t start with any word in the English dictionary, and it’s not a word in itself. Therefore we stop at this stage and back-track. The other possiblity is that the sentence starts with there, after which the next word could be is:
THERE IS somethingafoot
We essentially perform this same step over and over, until we reach one of three scenarios:
- We reach the end of the sentence composed of English words. This is a valid sentence:
THERE IS SOMETHING AFOOT - We reach a point where we cannot go any further in the sentence, as the remainder of the sentence couldn’t possibly be valid English:
THE REISS omethingafoot - We reach a point where there are no more full English words, but the last part could be an English word with more letters:
ELEVEN AND TWO IS THIRTEwould be valid with the lettersenat the end.
The pseudo-code to determine if something is a valid sentence in this way looks like this:
def ValidSentence(Sentence, WordsSoFar, EnglishWordList):
If Sentence = "":
Return New CompleteSentence(WordsSoFar)
Else:
PossibleWords := EnglishWordList.Filter(Word -> Sentence.StartsWith(Word))
If PossibleWords.IsEmpty:
PossibleIncompleteWords := EnglishWordList.Filter(Word -> Word.StartsWith(Sentence))
if PossibleIncompleteWords.IsEmpty:
Return []
Else:
Return New IncompleteSentence(WordsSoFar, PossibleIncompleteWords)
Else:
Return PossibleWords
.Map(Word -> ValidSentence(Sentence.RemovePrefix(Word), WordsSoFar + Word, EnglishWordList)
.Flatten()
finding a path
Now we know how to tell a valid sentence apart from gibberish, we need to find these valid sentences inside the grid. The way I solved this was to just do a depth first search on every possible path, stopping only when a definitely-invalid sequence of characters is reached. This animation might do it some justice:

You can probably deduce the pseudo-code for this yourself: it’s just a trial-and-error process. Whenever an invalid sentence, cycle or dead end is found, the search stops and back-tracks to the last valid state. All of this searching leads to a whopper of a call stack, making it quite nasty to debug.
the solution
I wrote the solution twice. The first time I solved it in Ruby here. This works, but it’s fairly bog-standard and quite slow. The second time round, I solved it in Haskell here, which took quite a lot of staring-at-screen debugging, but I got there eventually. Here’s the lightly-annotated code, if you’re interested:
import Control.Monad
import Data.Array
import Data.Char
import Data.List
import Data.Ord
import System.Environment
import System.IO
type GridLine = Array Int Char
type Grid = Array Int GridLine
-- Sentence data structure
data Sentence = Total [String]
| Partial [String] String
| Invalid deriving (Eq)
-- This is so we can print sentences
instance Show Sentence where
show (Total w) = map toUpper $ unwords $ w
show (Partial w t) = (map toUpper $ unwords $ w) ++ " " ++ t ++ "?"
show (Invalid) = "Invalid"
-- Strip non-alphabetic characters, and put into lower case
sanitise :: String -> String
sanitise = (map toLower) . (filter isLetter)
-- Reads the first line of input. Discards first number because we do not
-- need it. Reads 2nd and 3rd numbers as starting point co-ordinates
getStart :: String -> (Int, Int)
getStart s = (s' !! 1, s' !! 2) where s' = map read $ words s
-- Converts a list into a 1-indexed array
getGridArray :: [a] -> Array Int a
getGridArray xs = listArray (1, length xs) xs
-- Gets the boundaries (Width, Height) of a 2-D array
getGridBound :: Grid -> (Int, Int)
getGridBound g = let (y1, y2) = bounds g
(x1, x2) = bounds (g ! y1)
in (x2, y2)
-- Resolves a sentence into a list of possible combinations of words or
-- partial words by a nasty definitely-not-polynomial algorithm
resolve :: [String] -> String -> [Sentence]
resolve wl s = resolveR (sanitise s) [] where
resolveR [] acc = [Total (reverse acc)]
resolveR s acc = let ws = sortBy (comparing $ negate . length) $ filter (`isPrefixOf` s) wl
in if null ws
then let partials = filter (isPrefixOf s) wl
in if null partials
then []
else [Partial (reverse acc) $ head partials]
else foldr1 (++) $ map (\w -> resolveR (s \\ w) (w : acc)) ws
-- Unpacks a string by recursively traversing the grid on every possible
-- Hamiltonian path, and only stopping when the resulting sentence is not
-- valid (cannot be resolved). Hence, this is O(4^n) in the worst case
unpack :: [String] -> Grid -> (Int, Int) -> Sentence
unpack wl g s = unpackR [] [] s where
(w, h) = getGridBound g
unpackR s v (x, y)
| x < 1 || y < 1 || x > w || y > h = Invalid
| (x, y) `elem` v = Invalid
| otherwise
= let s' = s ++ [g ! y ! x]
rs = resolve wl s'
in if null rs
then Invalid
else let v' = (x, y) : v
vn = [(x-1, y), (x+1, y), (x, y-1), (x, y+1)]
in if length v' == w * h
then head rs
else
case filter ((/=) Invalid) $
map (unpackR s' v') vn of
Invalid -> Invalid
(s:_) -> s
-- Handles I/O - can you tell that I just found out about fmap and monads?
main :: IO ()
main = do args <- getArgs
words <- fmap (map sanitise . lines) $ readFile $ head args
start <- fmap getStart $ getLine
grid <- fmap (getGridArray . map (getGridArray . sanitise) . lines) getContents
putStrLn $ show $ unpack words grid startThe resolve Haskell function above is the same as the ValidSentence pseudo-code we looked at earlier - you can probably see the resemblance. Leave a comment if you’ve got any questions regarding the solution or the challenge.